【世紀難題】2名電腦科學家聯手開發切蛋糕演算法，多少人吃也能完美平分

By cherry.liu on 14 Oct 2016

切蛋糕看似是一件簡單非常的事情，但要完美地平分給所有人則是一件世紀難事。這件表面簡單實際苦難的事在過去也曾激起很多科學家的興趣，而過去的研究都紛紛帶出完美平分是不可能的結論。這個結論到今天就要被打破了，因為兩名來自美國的科學家聲稱他們發明了一條能在任何情況下完美平分蛋糕的演算法。

Photo from Quanta Magazine

去年4月，兩名美國電腦科學家在網上發佈了一篇論文，描述了他們所發明的一條切蛋糕演算法。這條演算法不以每人的喜好作計算標準，而是按照食用人數而定。這兩名科學家分別為美國卡內基梅隆大學（Carnegie Mellon）的研究員Simon Mackenzie以及澳洲新南威爾士大學（University of New South Wales）的電腦科學家Haris Aziz。曾就有關議題進行研究的電腦科學家Ariel Procacia則表示，有關成果對於學習公平分配博弈理論（Theory of fair division）的人來說是本世紀最大的成果。

Aziz和Mackenzie的新演算法建基於一條由數學家John Selfridge及John Conway分別在1960年代所構想出來的計算程序。這條計算法的前提是把蛋糕於3人之間平分。

Photo from Delish

那麽1960年代的計算法是如何進行呢？假設有3個人想平分一個蛋糕（A、B、C）。演算法會首先邀請C切出他認為是平均的分量，然後讓A和B決定他們想要的那一塊蛋糕。如果A和B都能選到心儀的那一塊，那就皆大歡喜。如果A和B的心儀蛋糕是同一件的話，B就需要把那件蛋糕稍微切開，使剩餘的蛋糕符合他的第二選擇。這時，A就可以在這三件蛋糕中選他想要的。如果A沒有選剛才經B修剪的蛋糕，B則一定要選他剛修剪的那件蛋糕。剩餘的兩件蛋糕就由A和C先後選擇。

由於A是首先選擇的那一個，所以他能在分蛋糕一事上得到滿足；B由於能在他的兩個首選中選擇所以也能滿足。至於無論C選哪一件都好都能得到滿足，因為在他眼中這三件蛋糕是相等的。

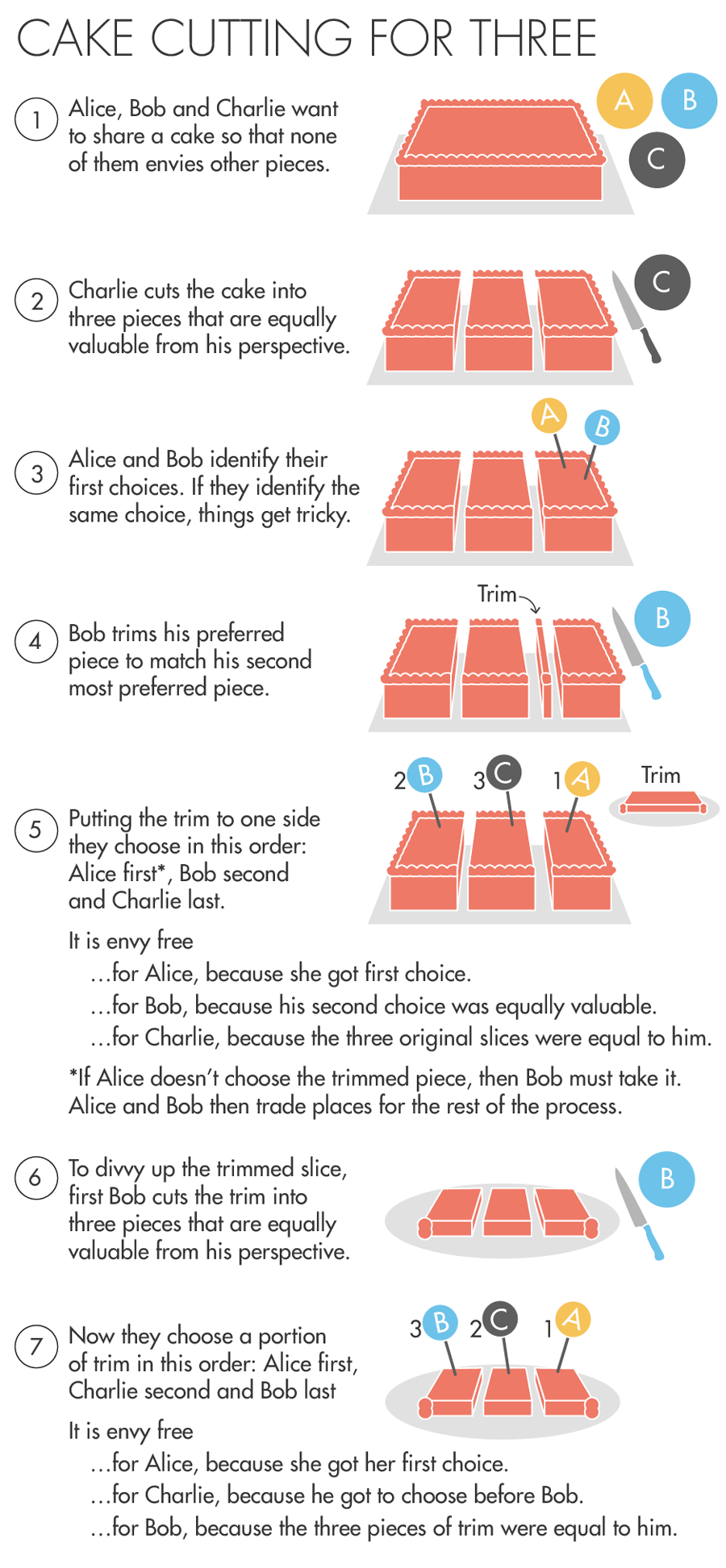Photo from Quanta Magazine

這看似一個有效的解決方法，但Selfridge和Conwa就無法把這個計算法推演成為分支定界法（Bound algorithm）；如果分蛋糕的不止3個人，那就不能完美地平分蛋糕了。Aziz和Mackenzie於是就修改了計算的程序，例如要求參加者把蛋糕分成若干塊相等的蛋糕，然後讓其他參加者選擇。此外，他們更把蛋糕分量比喻成注碼，並透過調整參加者之間的注碼，影響互相的統治關係（domination relationship）。

透過調整注碼而影響互相的統治關係，Aziz和Mackenzie就成功減低了問題的複雜性。比如説，若干參加者中如有3個人能統治其他參加者的選擇，他們就可以先選擇他們心儀的分量，然後從之後的程序中摒除 — 無論剩餘的人如何怎麽選擇，他們都已經選到了心儀的蛋糕。只要重覆執行這步驟，所有人就會得到自己想要的蛋糕而感到滿足。

Photo from Puzzlersworld

Procacia表示，由於演算法非常複雜，所以經過這麽久的時間才找到解決方法是完全不意外的。不過，Aziz和Mackenzie則認為他們可以簡化演算法，並正在撰寫成果。同樣進行過相關研究的Walter Stromquist教授表示，兩人的成果為研究切蛋糕的數學家和電腦科學家帶來了新的研究方向。Procaccia又指出，目前兩人需要做的就是算出這個新方法需要切多少刀才能平分這個蛋糕。